1.

(1)
模型的发现:
(2)
模型的迁移1:位置的改变
(3)
模型的迁移2:角度的改变
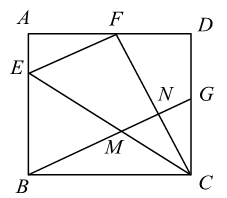
如图1,在中,
,
, 直线
经过点
, 且
、
两点在直线
的同侧,
直线
,
直线
, 垂足分别为点
,
. 请直接写出
、
和
的数量关系.
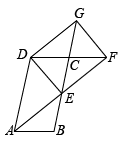
如图2,在(1)的条件下,若 ,
两点在直线
的异侧,请说明
、
和
的关系,并证明.
如图3,在(1)的条件下,若三个直角都变为了相等的钝角,即 , 其中
, (1)的结论还成立吗?若成立,请你给出证明;若不成立,请说明
、
和
的关系,并证明.
【考点】
三角形全等的判定-AAS;
能力提升
真题演练