如图，线段DE与AF分别为△ABC的中位线与中线.

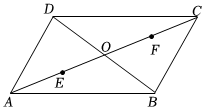
1. 如图，线段DE与AF分别为△ABC的中位线与中线.

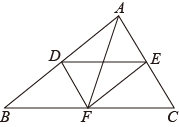
(1) 求证：AF与DE互相平分；

(2) 当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由.

【考点】

三角形的角平分线、中线和高; 平行四边形的判定与性质; 矩形的性质; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，平行四边形 $\text{[math]}$ ，对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两个动点，点 $\text{[math]}$ 从点 $\text{[math]}$ 开始向点 $\text{[math]}$ 匀速运动，点 $\text{[math]}$ 从点 $\text{[math]}$ 开始向点 $\text{[math]}$ 匀速运动，点 $\text{[math]}$ 和点 $\text{[math]}$ 同时出发，且运动速度均为 $\text{[math]}$ ．

(1) 求证：当 $\text{[math]}$ 、 $\text{[math]}$ 运动过程中不与点 $\text{[math]}$ 重合时，四边形 $\text{[math]}$ 是平行四边形；

(2) 若四边形 $\text{[math]}$ 为矩形，求动点 $\text{[math]}$ 、 $\text{[math]}$ 运动时间．

综合题困难

2. 如图，已知四边形ABCD，AD∥BC，对角线AC、BD交于点O，DO＝BO，过点C作CE⊥AC，交BD的延长线于点E，交AD的延长线于点F，且满足∠DCE＝∠ACB．

(1) 求证：四边形ABCD是矩形；

(2) 求证： $\text{[math]}$ ．

综合题普通

3. 已知，平行四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 向两个方向延长，分别至点 $\text{[math]}$ 和点 $\text{[math]}$ ，且使 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) 如图1，求证：四边形 $\text{[math]}$ 是平行四边形．

(2) 如图2，当 $\text{[math]}$ 时，在不添加任何辅助线情况下，请直接写出图2中的四个三角形，使写出的每个三角形面积都等于三角形 $\text{[math]}$ 面积的 $\text{[math]}$ ．

综合题普通