1.
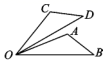
“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知 的周长为
的周长为 ,
,  . 制作该风筝框架需用材料的总长度至少为( )
. 制作该风筝框架需用材料的总长度至少为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练