1.
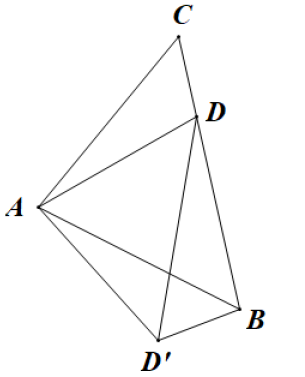
如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D .

(1)
求证:BE=CF;
(2)
当四边形ABDF为菱形时,求CD的长.
【考点】
旋转的性质;
三角形全等的判定-SAS;