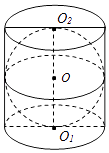
1.
在
中，
、
、
分别为内角
、
、
的对边，且
， 分别以
、
、
所在直线为轴，其余各边旋转一周形成的曲面围成3个几何体，其体积分别记为
、
、
．
(1)
求证：
；
(2)
求以所在直线为轴旋转所形成几何体的内切球的体积．
【考点】
旋转体（圆柱/圆锥/圆台/球）的结构特征;
球的表面积与体积公式及应用;
能力提升
真题演练
