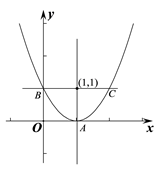1.
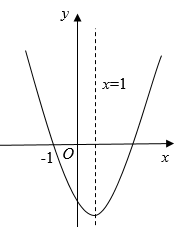
如图,直角坐标系中,抛物线 分别交
分别交 轴于点
轴于点 , 交
, 交 轴于点
轴于点 ,
,  (点
(点 在点
在点 的左侧),
的左侧), 为顶点,
为顶点, 为线段
为线段 上一点,过点
上一点,过点 作
作 轴的平行线分别交抛物线于点
轴的平行线分别交抛物线于点 ,
,  (点
(点 在点
在点 的左侧).
的左侧).

(1)
求该抛物线的对称轴及 的长.
(2)
当
的长.
(2)
当 时,点
时,点 关于
关于 的对称点
的对称点 恰好落在
恰好落在 轴上,求此时
轴上,求此时 的长.
的长.
【考点】
二次函数图象与坐标轴的交点问题;
二次函数图象上点的坐标特征;
二次函数y=ax²+bx+c的图象;
能力提升
真题演练