0 返回首页
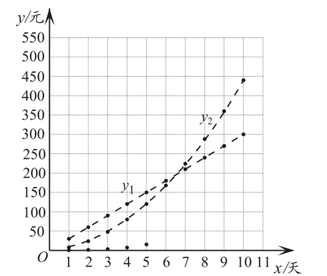
1. 在函数的学习中，我们经历了“确定函数表达式、画函数图象、利用函数图象研究函数性质”的学习过程下表是一个函数的自变量与函数值的部分对应值，请你借鉴以往学习函数的经验，探究下列问题：

0.5

1

2

3

4

5

6

2.5

2

2.5

3.3

4.3

5.2

6.2

(1) 当时，.
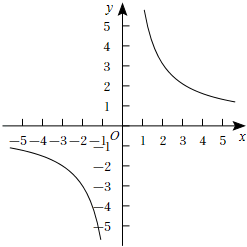
(2) 根据表中数值描点并画出函数图象；
(3) 观察画出的函数图象，写出这个函数的一条性质
【考点】
描点法画函数图象;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图1，△ABC是等腰直角三角形，∠A＝90°，BC＝4cm，点P在△ABC的边上沿路径B→A→C移动，过点P作PD⊥BC于点D，设BD＝xcm，△BDP的面积为ycm2（当点P与点B或点C重合时，y的值为0）.

小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.

下面是小东的探究过程，请补充完整：

(1) 自变量x的取值范围是；
(2) 通过取点、画图、测量，得到了x与y的几组值，如下表：

x/cm

0

1

2

3

4

y/cm2

0

m

2

n

0

请直接写出m＝ ， n＝；
(3) 如图2，在平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
(4) 结合画出的函数图象，解决问题：当△BDP的面积为1cm2时，BD的长度约为cm.（数值保留一位小数）
综合题 普通
2. 如图1，Rt△ABC中，∠ACB＝90°，点D为AB边上的动点（点D不与点A，点B重合），过点D作ED⊥CD交直线AC于点E，已知∠A＝30°，AB＝4cm，在点D由点A到点B运动的过程中，设AD＝xcm，AE＝ycm.

小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究.

下面是小东的探究过程，请补充完整：

(1) 通过取点、画图、测量，得到了x与y的几组值，如下表：

x/cm

…

1

2

3

…

y/cm

…

0.4

0.8

1.0

    

1.0

0

4.0

…

（说明：补全表格时相关数值保留一位小数）
(2) 在如图2的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
(3) 结合画出的函数图象，解决问题：当AE＝ AD时，AD的长度约为cm.
综合题 普通
3. 小腾的爸爸计划将一笔资金用于不超过10天的短期投资，针对这笔资金，银行专属客户经理提供了三种投资方案，这三种方案的回报如下：

方案一：每一天回报30元；

方案二：第一天回报8元，以后每一天比前一天多回报8元；

方案三：第一天回报0.5元，以后每一天的回报是前一天的2倍．

下面是小腾帮助爸爸选择方案的探究过程，请补充完整：

(1) 确定不同天数所得回报金额（不足一天按一天计算），如下表：

天数

1

2

3

4

5

6

7

8

9

10

方案一

30

30

30

30

30

30

30

30

30

30

方案二

8

16

24

32

40

48

56

64

72

80

方案三

0.5

1

2

4

8

16

32

64

128

其中 ；
(2) 计算累计回报金额，设投资天数为x（单位：天），所得累计回报金额是y（单位：元），于是得到三种方案的累计回报金额 ， ， 与投资天数x的几组对应值：

1

2

3

4

5

6

7

8

9

10

30

60

90

120

150

180

210

240

270

300

8

24

48

80

120

168

224

288

360

440

0.5

1.5

3.5

7.5

15.5

31.5

63.5

127.5

255.5

其中 ；
(3) 在同一平面直角坐标系 中，描出补全后的表中各组数值所对应的点 ， ， ，并画出 ， ， 的图象；

注：为了便于分析，用虚线连接离散的点．
(4) 结合图象，小腾给出了依据不同的天数而选择对应方案的建议：

综合题 普通