1.
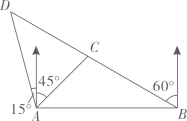
如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,sinB=  ,求:
,求:

(1)
线段DC的长;
(2)
sin∠EDC的值.
【考点】
勾股定理;
锐角三角函数的定义;