1.
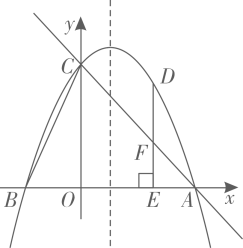
如图,抛物线  与
与  轴交于除原点
轴交于除原点  和点
和点  ,且其顶点
,且其顶点  关于
关于  轴的对称点坐标为
轴的对称点坐标为  .
.
(1)
求抛物线的函数表达式;
(2)
抛物线的对称轴上存在定点F,使得抛物线  上的任意一点G到定点F的距离与点G到直线
上的任意一点G到定点F的距离与点G到直线  的距离总相等.
(3)
点
的距离总相等.
(3)
点  是该抛物线上的一点,在x轴,y轴上分别找点
是该抛物线上的一点,在x轴,y轴上分别找点  ,使四边形
,使四边形  周长最小,直接写出
周长最小,直接写出  的坐标.
的坐标.
①证明上述结论并求出点F的坐标;
②过点F的直线l与抛物线 交于
两点.证明:当直线l绕点F旋转时,
是定值,并求出该定值;
【考点】
待定系数法求二次函数解析式;
二次函数-动态几何问题;
真题演练