1.
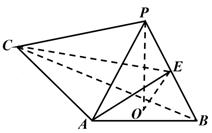
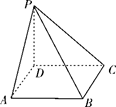
已知四棱锥  的底面为直角梯形,
的底面为直角梯形,  ,
,  ,
,  ,
,  ,
,  平面
平面  ,且
,且  ,平面
,平面  与平面
与平面  的交线为
的交线为  .
.

(1)
求证:  ;
(2)
试建立适当的空间直角坐标系,并求点
;
(2)
试建立适当的空间直角坐标系,并求点  在平面
在平面  上的射影
上的射影  的坐标.
的坐标.
【考点】
直线与平面平行的判定;
直线与平面平行的性质;