1.
 和
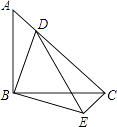
和  都是等边三角形,
都是等边三角形,  绕点C旋转,连接
绕点C旋转,连接  .
.

(1)
猜测发现
:如图1,  与
与  是否相等?若相等,加以证明;若不相等,请说明理由.
(2)
问题解决
:若
是否相等?若相等,加以证明;若不相等,请说明理由.
(2)
问题解决
:若  三点不在一条直线上,且
三点不在一条直线上,且  ,求
,求  的长.
(3)
拓展运用
:若
的长.
(3)
拓展运用
:若  三点在一条直线上(如图2),且
三点在一条直线上(如图2),且  和
和  的边长分别为1和2,
的边长分别为1和2,  的面积及
的面积及  的值.
的值.
【考点】
等边三角形的性质;
旋转的性质;