1.
教材呈现：如图是华师版九年级上册数学教材第103页的部分内容．
已知：如图①，在 中，
，
是斜边
上的中线．求证：
．
(1)
请写出完整的证明过程．
(2)
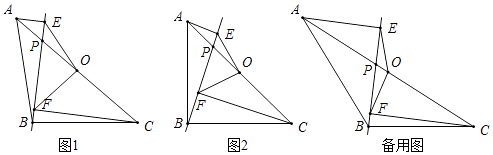
结论应用：如图②， 
、 
是锐角 
的两条高，M、N分别是 
、 
的中点，判断 与 
的位置关系，并证明你的结论．
(3)
在（2）的条件下，若 
，则 的长为．
【考点】
等腰三角形的判定与性质;
直角三角形斜边上的中线;
