1.
在△ABC中，AB=BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．
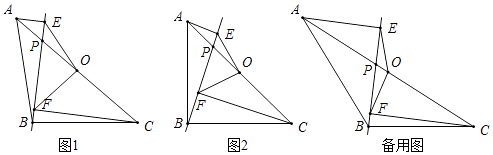
(1)
如图1，请直接写出线段OE与OF的数量关系；
(2)
如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由
(3)
若|CF﹣AE|=2，EF=2 
，当△POF为等腰三角形时，请直接写出线段OP的长．
【考点】
全等三角形的判定与性质;
等腰三角形的判定与性质;
直角三角形斜边上的中线;
