0 返回首页
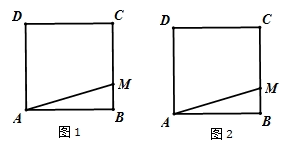
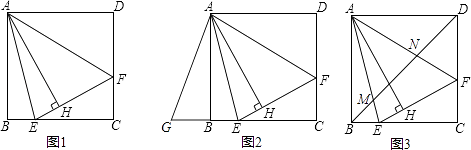
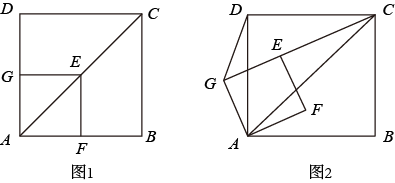
1. 如图，正方形ABCD中，直线a经过点A，且BE⊥a于E，DF⊥a于F.

(1) 当直线a绕点A旋转到图1的位置时，求证：①△ABE≌△DAF；②EF＝BE+DF；
(2) 当直线a绕点A旋转到图2的位置时，试探究EF、BE、DF具有怎样的等量关系？请写出这个等量关系，并加以证明；
(3) 当直线a绕点A旋转到图3的位置时，试问DF、EF、BE具有怎样的等量关系？请写出这个等量关系，不证明.
【考点】
正方形的性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如果AF=4，AB=7．

(1) 求BE的长；
(2) 在图中作出延长BE与DF的交点G，并说明BG⊥DF．
综合题 普通
2. 如图，在正方形ABCD中，点M是BC边上任意一点，请你仅用无刻度直尺，分别在图1、图2中按要求作图(保留作图痕迹，不这写作法)

(1) 在图1中，在AB边上求作一点N，连接CN，使得CN=AM；
(2) 在图2 中，在AD边上求作一点Q，连接CQ，使得CQ=AM．
综合题 普通
3. 如图1，把△ABC沿直线BC平移线段BC的长度，得到△ECD；如图2，以BC为轴，把△ABC沿BC翻折180°，可以得到△DBC；如图3，以点A为中心，把△ABC旋转180°，可以得到△AED ． 像这样，其中一个三角形是由另一个三角形按平移、翻折、旋转等方法得到的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．回答下列问题：

(1) 在图4中，可以使△ABE通过平移、翻折、旋转中的哪一种方法得到△ADF？
(2) 图中线段BE与DF相等吗？为什么？
综合题 普通