1.
等边三角形  的边长为3,点
的边长为3,点  、
、  分别是边
分别是边  、
、  上的点,且满足
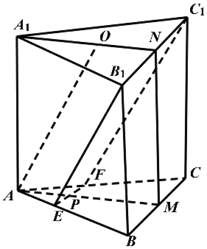
上的点,且满足  (如图1).将
(如图1).将  沿
沿  折起到
折起到  的位置,使二面角
的位置,使二面角  成直二面角,连结
成直二面角,连结  、
、  (如图2).
(如图2).

(1)
求证:  平面
平面  ;
(2)
在线段
;
(2)
在线段  上是否存在点
上是否存在点  ,使直线
,使直线  与平面
与平面  所成的角为
所成的角为  ?若存在,求出
?若存在,求出  的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
【考点】
直线与平面垂直的判定;
直线与平面所成的角;