如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.

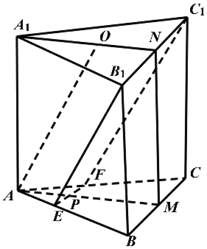
1. 如图，已知三棱柱ABC-A₁B₁C₁的底面是正三角形，侧面BB₁C₁C是矩形，M，N分别为BC，B₁C₁的中点，P为AM上一点，过B₁C₁和P的平面交AB于E，交AC于F.

(1) 证明：AA₁∥MN，且平面A₁AMN⊥EB₁C₁F；

(2) 设O为△A₁B₁C₁的中心，若AO∥平面EB₁C₁F，且AO=AB，求直线B₁E与平面A₁AMN所成角的正弦值.

【考点】

平行公理; 直线与平面垂直的判定; 平面与平面垂直的判定; 直线与平面所成的角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在三棱台 $\text{[math]}$ 中，上下底面分别是边长为2和4的正三角形， $\text{[math]}$ 平面 $\text{[math]}$ .设平面 $\text{[math]}$ 平面 $\text{[math]}$ ，点 $\text{[math]}$ 分别在直线 $\text{[math]}$ 和直线 $\text{[math]}$ 上，且满足 $\text{[math]}$ .

(1) 证明： $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 若直线 $\text{[math]}$ 和平面 $\text{[math]}$ 所成角的正弦值为 $\text{[math]}$ ，求该三棱台的高.

解答题普通

2. 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 为平行四边形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 若二面角 $\text{[math]}$ 的大小为 $\text{[math]}$ ，点 $\text{[math]}$ 在棱 $\text{[math]}$ 上，且 $\text{[math]}$ ，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值．

解答题普通

3. 如图，在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ，证明：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正切值的最小值．

解答题普通