1.
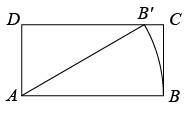
如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.

(1)
求证:∠CBE=  ∠BAE;
(2)
求证:PG=PB;
(3)
若AB=
∠BAE;
(2)
求证:PG=PB;
(3)
若AB=  ,BC=3,求出BG的长.
,BC=3,求出BG的长.
【考点】
矩形的性质;
旋转的性质;
能力提升
真题演练