0 返回首页
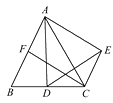
1. 如图，在等边三角形ABC中，点D是BC边的中点，以AD为边作等边三角形ADE.

(1) 求∠CAE的度数；
(2) 取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形．
【考点】
矩形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若 ，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且 ， ．

理解与作图：

(1) 在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．

计算与猜想：
(2) 求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？

启发与证明：
(3) 如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．
综合题 普通