0 返回首页
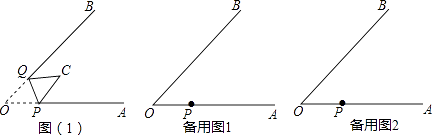
1. 两个全等的△ABC和△DEF重叠在一起，固定△ABC，将△DEF进行如下变换：

(1)

如图1，△DEF沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD，请直接写出S△ABC与S四边形AFBD的关系；
(2)

如图2，当点F平移到线段BC的中点时，四边形AFBD是什么特殊四边形？请给出证明；
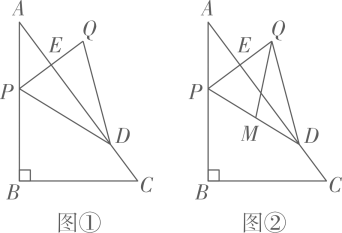
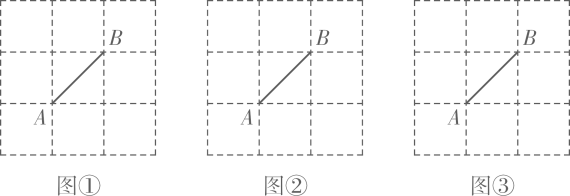
(3) 当点F平移到线段BC的中点时，若四边形AFBD为正方形，猜想△ABC应满足什么条件？请直接写出结论：在此条件下，将△DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请在图3位置画出图形，并求出sin∠CGF的值．
【考点】
三角形相关概念;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 在现实生活中，我们会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为 ：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P为DC边上一定点，且CP=BC，如图所示．

(1)

如图①，求证：BA=BP；
(2)

如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求 的值；
(3)

如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．
综合题 普通
2.

如图（1），∠AOB=45°，点P、Q分别是边OA，OB上的两点，且OP=2cm．将∠O沿PQ折叠，点O落在平面内点C处．

(1) 当PC∥QB时，OQ=；
(2) 当PC⊥QB时，求OQ的长．
(3) 当折叠后重叠部分为等腰三角形时，求OQ的长．
综合题 困难
3.

如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上的一动点，连接CD，DE，以CD，DE为边作▱CDEF．

(1) 当0＜m＜8时，求CE的长（用含m的代数式表示）；
(2) 当m=3时，是否存在点D，使▱CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；
(3) 点D在整个运动过程中，若存在唯一的位置，使得▱CDEF为矩形，请求出所有满足条件的m的值．
综合题 困难