1.
（问题背景）在一条直线上有n个点（n≥2），每两个点确定一条线段，一共有多少条线段？（请在答题卡上按照序号顺序解决问题）
(1)
（探究）当仅有2个点时，有 
=1条线段；
(2)
（应用）
(3)
（拓展）平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少个不同的三角形？
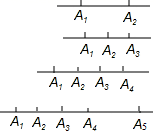
当有3个点时，有 =3条线段；
当有4个点时，有 =6条线段；
①当有5个点时，有条线段；
……
②当有n个点时，从这些点中任意取一点，如图，以这个点为端点和其余各点能组成（n－1）条线段，这样总共有n（n－1）条线段.在这些线段中每条线段都重复了两次，如：线段A1A2和A2A1是同一条线段，所以，一条直线上有n个点，一共有Sn=条线段.
③在一条直线上有10个点，直线外一点分别与这10个点连接成线段，一共可以组成个三角形.
④平面上有50个点，且任意三个点不在同一直线上，过这些点作直线，一共能作出条不同的直线.
当有3个点时，可作1个三角形；
⑤当有4个点时，可作个三角形；
⑥当有5个点时，可作个三角形；
……
⑦当有n个点时，可连成个三角形.
【考点】
探索图形规律;
