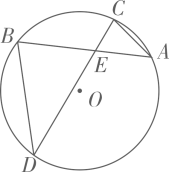1.
用两种方法证明“圆的内接四边形对角互补”.
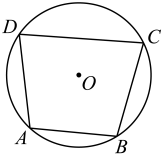
已知:如图①,四边形ABCD内接于⊙O.
求证:∠B+∠D=180°.


证法1:如图②,作直径DE交⊙O于点E,连接AE、CE.
∵DE是⊙O的直径,
∴( ).
∵∠DAE+∠AEC+∠DCE+∠ADC=360°,
∴∠AEC+∠ADC=360°-∠DAE-∠DCE=360°-90°-90°=180°.
∵∠B和∠AEC所对的弧是 ,
∴( ).
∴∠B+∠ADC=180°.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
【考点】
圆周角定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练