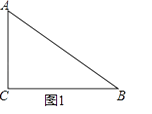
如图1，在△ABC中，AB=AC=2，∠A=90°，将一块与△ABC全等的三角板的直角顶点放在点C上，一直角边与BC重叠．

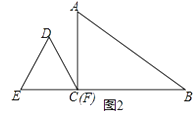
(1) 操作1：固定△ABC，将三角板沿C→B方向平移，使其直角顶点落在BC的中点M，如图2所示，探究：三角板沿C→B方向平移的距离为；

(2)

操作2：在（1）的情况下，将三角板BC的中点M顺时针方向旋转角度a（0°＜a＜90°），如图3所示，探究：设三角形板两直角边分别与AB、AC交于点P、Q，观察四边形MPAQ形状的变化，问：四边形MPAQ的面积S是否改变，若不变，求其面积；若改变，试说明理由；

(3) 在（2）的情形下，连PQ，则当△MPQ的面积等于四边形MPAQ的面积的一半时，四边形MPAQ的形状为，此时BP=．

【考点】

三角形的面积; 相似三角形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

如图（1）在Rt△ABC中，∠C=90°，AB=5cm．BC=a cm，AC=3cm，且a是方程x²﹣（m﹣1）x+m+4=0的根．

(1) 求a和m的值；

(2)

如图（2），有一个边长为 $\text{[math]}$ 的等边三角形DEF从C出发，以1cm/s的速度沿CB方向移动，至△DEF全部进入与△ABC为止，设移动时间为xs，△DEF与△ABC重叠部分面积为y，试求出y与x的函数关系式并注明x的取值范围；

(3) 试求出发后多久，点D在线段AB上？

综合题困难

已知：如图，在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，点P从点B出发，沿BC向点C匀速运动，速度为1cm/s；过点P作PD∥AB，交AC于点D，同时，点Q从点A出发，沿AB向点B匀速运动，速度为2cm/s；当一个点停止运动时，另一个点也停止运动，连接PQ．设运动时间为t（s）（0＜t＜2.5），解答下列问题：

(1) 当t为何值时，四边形ADPQ为平行四边形？

(2) 设四边形ADPQ的面积为y（cm²），试确定y与t的函数关系式；

(3) 在运动过程中，是否存在某一时刻t，使S_四边形_ADPQ：S_△_PQB=13：2？若存在，请说明理由，若存在，求出t的值，并求出此时PQ的距离．

综合题困难

如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动，同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动，过点P作PD⊥BC，交AB于点D，连接PQ．当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．

(1) 当a=2时，解答下列问题：

①QB=，PD=．（用含t的代数式分别表示）

(2) 当a为某个数值时，四边形PDBQ在某一时刻为菱形，求a的值及四边形PDBQ为菱形时t的值．

(3) 当t=2时，在整个运动过程中，恰好存在线段PQ的中点M到△ABC三边距离相等，直接写出此刻a的值．

综合题普通