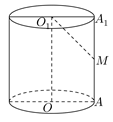
如图，我们知道，圆锥是（及其内部）绕所在的直线旋转一周形成的几何体.我们现将直角梯形（及其内部）绕所在的直线旋转一周形成的几何体称为圆台.设的半径为，的半径为， .

1. 如图，我们知道，圆锥是 $\text{[math]}$ （及其内部）绕 $\text{[math]}$ 所在的直线旋转一周形成的几何体.我们现将直角梯形 $\text{[math]}$ （及其内部）绕 $\text{[math]}$ 所在的直线旋转一周形成的几何体称为圆台.设 $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ 的半径为 $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证：圆台的体积 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求圆台的表面积S.

【考点】

棱柱/棱锥/棱台的侧面积、表面积及应用; 棱柱、棱锥、棱台的体积;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 现有四个正四棱柱形容器，1号容器的底面边长是a，高是b；2号容器的底面边长是b，高是a；3号容器的底面边长是a，高是a；4号容器的底面边长是b，高是b.假设 $\text{[math]}$ ，问是否存在一种必胜的4选2的方案（与 $\text{[math]}$ 的大小无关），使选中的两个容器的容积之和大于余下的两个容器的容积之和？无论是否存在必胜的方案，都要说明理由.

解答题普通

2. 已知P是底面为正三角形的直三棱柱 $\text{[math]}$ 的上底面 $\text{[math]}$ 的中心，作平面 $\text{[math]}$ 与棱 $\text{[math]}$ 交于点D．若 $\text{[math]}$ ，则三棱锥 $\text{[math]}$ 的体积为．

解答题普通

3. 如图，正方体 $\text{[math]}$ 的所有棱长都为1，求点A到平面 $\text{[math]}$ 的距离.

解答题普通