1.
如图(1),大正方形的面积可以表示为  ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即
,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即  .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:
.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:  .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”
.把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”

(1)
用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:;
(2)
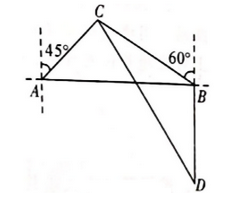
如图(3),  中,
中,  ,
,  ,
,  ,
,  是斜边
是斜边  边上的高.用上述“面积法”求
边上的高.用上述“面积法”求  的长;
(3)
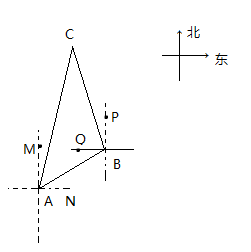
如图(4),等腰
的长;
(3)
如图(4),等腰  中,
中,  ,点O为底边
,点O为底边  上任意一点,
上任意一点,  ,
,  ,
,  ,垂足分别为点M,N,H,连接
,垂足分别为点M,N,H,连接  ,用上述“面积法”,求证:
,用上述“面积法”,求证:  .
.



【考点】
三角形的面积;
勾股定理的应用;
能力提升
真题演练