1.
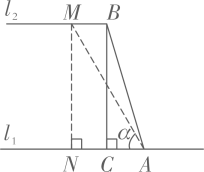
如图,一个梯子  斜靠在一面墙上,梯子底端为A,梯子的顶端B距地面的垂直距离为
斜靠在一面墙上,梯子底端为A,梯子的顶端B距地面的垂直距离为  的长.
的长.

(1)
若梯子的长度是  ,梯子的顶端B距地面的垂直距离为
,梯子的顶端B距地面的垂直距离为  .如果梯子的顶端下滑
.如果梯子的顶端下滑  ,那么梯子的底端A向外滑动多少米?
(2)
设
,那么梯子的底端A向外滑动多少米?
(2)
设  ,
,  ,
,  ,且
,且  ,请思考,梯子在滑动的过程中,是否一定存在顶端下滑的距离与底端向外滑动的距离相等的情况?若存在,请求出这个距离;若不存在,说明理由.
,请思考,梯子在滑动的过程中,是否一定存在顶端下滑的距离与底端向外滑动的距离相等的情况?若存在,请求出这个距离;若不存在,说明理由.
【考点】
勾股定理的应用;
能力提升
真题演练