1.
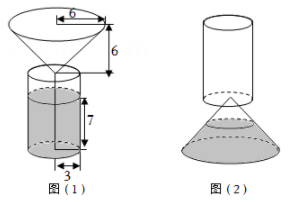
有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为.

【考点】
圆柱的体积;
基础巩固
拓展培优
真题演练