1.
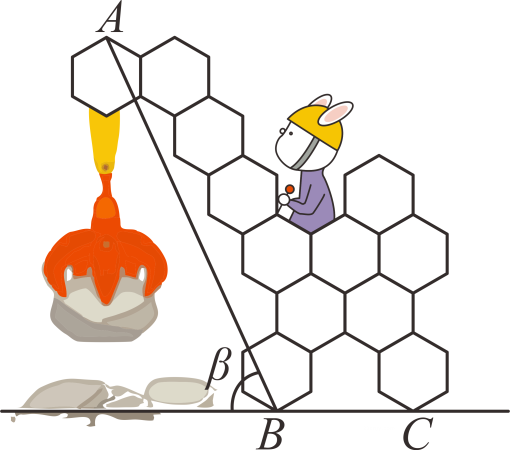
如图是小明画的卡通图形,每个正六边形的边长都相等,相邻两正六边形的边重合,点A,B,C均为正六边形的顶点,AB与地面BC所成的锐角为β,则tanβ的值是.
【考点】
圆内接正多边形;
解直角三角形的其他实际应用;






