0 返回首页
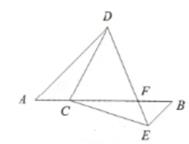
1. 如图，AB，DE交于点F，AD∥BE，点C在线段AB上，且AC=BE，AD=BC，连结CD，CE。

(1) 求证：∠ADC=∠BCE。
(2) 若∠A=40°，∠ADC=20°，求∠CDE的度数。
【考点】
全等三角形的判定与性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在△ABC中，AB=AC，点D，E分别在AC及其延长线上，点B，F分别在AE两侧，连结CF，已知AD=EC，BC=DF，BC∥DF。

(1) 求证：△ABC≌△EFD。
(2) 若CE=CF，FC平分∠DFE，求∠A的度数。
综合题 普通
2. 如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O.

(1) 求证：△AEC≌△BED；
(2) 若∠1＝50°，则∠BDE＝°.
综合题 普通
3. 在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=α(0°<α≤90°)，点F，G，P分别是DE，BC，CD的中点，连接PF，PG。

(1) 如图①，α=90°，点D在AB上，则∠FPG=°
(2) 如图②，α=60°，点D不在AB上，判断∠FPG的度数，并证明你的结论；
(3) 连接FG，若AB=5，AD=2，固定△ABC，将△ADE绕点A旋转，当PF的长最大时，FG的长为(用含α的式子表示)。
综合题 普通