1.
通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，先阅读再解决后面的问题：
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，求证：EF=BE+DF．
解题分析：由于AB=AD，我们可以延长CD到点G，使DG=BE，易得∠ABE=∠ADG=90°，可证△ABE≌△ADG
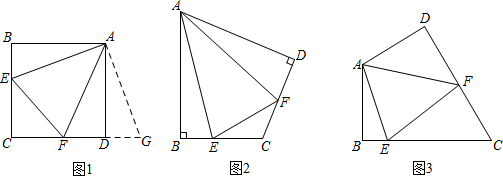
再证明△AFG≌△AFE，得EF=FG=DG+FD=BE+DF
(1)
如图2，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF= 
∠BAD．求证：EF=BE+FD；
(2)
如图3，在四边形ABCD中，∠B=∠D=90°，∠BAD=120°，AB=AD=1，点E、F分别在四边形ABCD的边BC、CD上，且∠EAF=60°，求此时△CEF的周长．
【考点】
全等三角形的判定与性质;
