1.
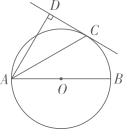
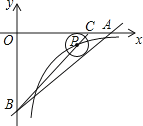
阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如图1∠ABC所示.同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图2)
证明:∵AB切⊙O于点A,∴∠CAB=90°,又∵AC是直径,∴∠P=90°∴∠CAB=∠P

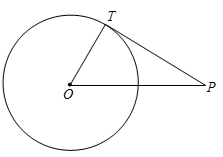
问题拓展:若AC不经过圆心O(如图3),该结论:弦切角∠CAB=∠P还成立吗?请说明理由.
知识运用:如图4,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC.
【考点】
切线的性质;
基础巩固
变式训练
拓展培优
真题演练