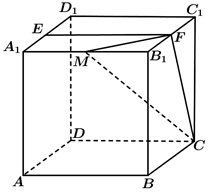
如图，在直三棱柱ABC﹣A1B1C1中，BC= ，AB=AC=AA1=1，D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1 ．

1. 如图，在直三棱柱ABC﹣A₁B₁C₁中，BC= $\text{[math]}$ ，AB=AC=AA₁=1，D是棱CC₁上的一点，P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA₁ ．

(1) 求证：CD=C₁D；

(2) 求二面角A₁﹣B₁D﹣P的平面角的正弦值．

【考点】

与二面角有关的立体几何综合题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知 $\text{[math]}$ 是棱长为 $\text{[math]}$ 的正四面体 $\text{[math]}$ ，设 $\text{[math]}$ 的四个顶点到平面 $\text{[math]}$ 的距离所构成的集合为 $\text{[math]}$ ，若 $\text{[math]}$ 中元素的个数为 $\text{[math]}$ ，则称 $\text{[math]}$ 为 $\text{[math]}$ 的 $\text{[math]}$ 阶等距平面， $\text{[math]}$ 为 $\text{[math]}$ 的 $\text{[math]}$ 阶等距集.

(1) 若 $\text{[math]}$ 为 $\text{[math]}$ 的1阶等距平面且1阶等距集为 $\text{[math]}$ ，求 $\text{[math]}$ 的所有可能值以及相应的 $\text{[math]}$ 的个数；

(2) 已知 $\text{[math]}$ 为 $\text{[math]}$ 的4阶等距平面，且点 $\text{[math]}$ 与点 $\text{[math]}$ 分别位于 $\text{[math]}$ 的两侧.若 $\text{[math]}$ 的4阶等距集为 $\text{[math]}$ ，其中点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为 $\text{[math]}$ ，求平面 $\text{[math]}$ 与 $\text{[math]}$ 夹角的余弦值.

解答题困难

2. 如图，点 $\text{[math]}$ 在 $\text{[math]}$ 内， $\text{[math]}$ 是三棱锥 $\text{[math]}$ 的高，且 $\text{[math]}$ ． $\text{[math]}$ 是边长为 $\text{[math]}$ 的正三角形， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点.

(1) 证明：点 $\text{[math]}$ 在 $\text{[math]}$ 上.

(2) 点 $\text{[math]}$ 是棱 $\text{[math]}$ 上的一点（不含端点），求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角余弦值的最大值.

解答题普通