1.
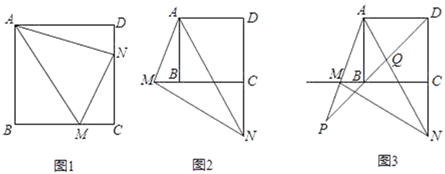
如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
(1)
如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)
如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)
如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
【考点】
全等三角形的判定与性质;
勾股定理;
正方形的性质;
相似三角形的判定与性质;