1.
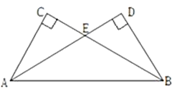
已知在△ABC与△ABD中,AC=BD , ∠C=∠D=90°,AD与BC交于点E ,

(1)
求证:AE=BE;
(2)
若AC=3,AB=5,求△ACE的周长.
【考点】
全等三角形的判定与性质;
勾股定理;
能力提升
真题演练