1.
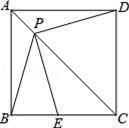
如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP.直线CE与线段AB相交于点F(点F与点A、B不重合)

(1)
求证:△AEP≌△CEP;
(2)
判断CF与AB的位置关系,并说明理由;
(3)
求△AEF的周长。
【考点】
全等三角形的判定与性质;
正方形的性质;
能力提升
真题演练