如图，∠A＝∠B ， AE＝BE ，点D在AC边上，∠1＝∠2，AE和BD相交于点O ．

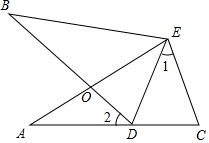
1. 如图，∠A＝∠B ， AE＝BE ，点D在AC边上，∠1＝∠2，AE和BD相交于点O ．

(1) 求证：△AEC≌△BED；

(2) 若∠1＝42°，求∠BDE的度数．

【考点】

全等三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．

(1) 求证：BD=CE；

(2) 求证：∠M=∠N．

综合题困难

2. 如图，在等腰Rt△ABC中，∠ACB＝90°，AC＝CB ， F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD＝CE ．连接DE、DF、EF ．

(1) 求证：△ADF≌△CEF；

(2) 试证明△DFE是等腰直角三角形．

综合题普通

3. 如图，在四边形ABCD中，AC平分∠BAD，且AC=BC，AB=2AD．

(1) 求∠ADC的度数；

(2) 若AB=10cm，CD=12cm，求四边形ABCD的面积．

综合题普通