通过如下尺规作图，能确定点D是BC边中点的是（）

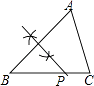
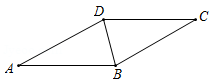
1. 通过如下尺规作图，能确定点D是BC边中点的是（）

A.

B.

C.

D.

【考点】

线段垂直平分线的性质; 尺规作图的概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别以A、B为圆心，两弧分别交于E、F，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点D，则 $\text{[math]}$ 的周长等于（　　）

A. 7 B. 8 C. 9 D. $\text{[math]}$

单选题容易

2. 如图，在 $\text{[math]}$ 中，按以下步骤作图：①分别以点B和C为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点M和N；②作直线MN交边AB于点E ，连接CE.若 $\text{[math]}$ ，则EC的长为（）

A. 16 B. 12 C. 10 D. 8

单选题容易

3. 如图，AD是 $\text{[math]}$ 的高线，则下列结论正确的是（）

A. 若 $\text{[math]}$ ，则 $\text{[math]}$ B. 若 $\text{[math]}$ ，则 $\text{[math]}$ C. 若 $\text{[math]}$ ，则 $\text{[math]}$ D. 若 $\text{[math]}$ ，则 $\text{[math]}$

单选题容易