1.
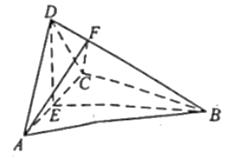
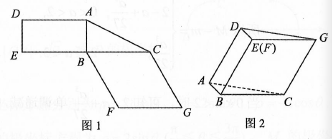
图1是由矩形ADEB、 
ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°.将其沿AB ， BC折起使得BE与BF重合，连结DG ， 如图2.
(1)
证明图2中的A ， C ， G ， D四点共面，且平面ABC⊥平面BCGE；
(2)
求图2中的四边形ACGD的面积.
【考点】
直线与平面垂直的判定;
平面与平面垂直的判定;
