0 返回首页
1. 【探究】
(1) 观察下列算式，并完成填空：

1=12

1+3=4=22

1+3+5=9=32

1+3+5+7=16=42

1+3+5+．……+(2n-1）=（n为正整数）
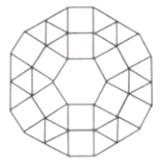
(2) 如图是某市一广场地面图案的一部分，图案的中央是一块正六边形的地砖，周围用正三角形和正方形的地砖铺成，环绕正兴动形的那些正三角形和正方形为第一层，第一层包括6块正方形和6块正三角形地砖：环绕第一层的那些正三角形和正方形为第二层，第二层包括6块正方形和18块正三角形地砖，以此递推。

①第3层包括块正方形利和块正三角形地砖；

②第n层包括块正三角形地砖（用含n的代数式表示）。
(3) 【应用】该市打算在一个新建广场中央采用如图所示的图案铺设地面，现有1块正六边形、150块正方形和2700块正三角形，问：铺设这样的图案，最多能铺多少层？请说明理由。
【考点】
探索图形规律;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
实践探究题 困难
能力提升
真题演练
换一批
1. 【探究】
(1) 观察下列算式，并完成填空：

1=12

1+3=4=22：

1+3+5=9=32：

1+3+5+7=16=42：

1+3+5+…+（2n-1）=．（n是正整数）
(2) 如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案，图案中央是一块正六边形地板砖，周围是正方形和正三角形的地板砖．从里向外第一层包括6块正方形和6块正三角形地板砖；第二层包括6块正方形和18块正三角形地板砖；以此递推。

①第3层中分别含有  ▲  块正方形和  ▲  块正三角形地板砖：

②第n层中含有  ▲  块正三角形地板砖（用含n的代数式表示）。

【应用】

该市打算在一个新建广场中央，采用图样式的图案铺设地面，现有1块正六边形、150块正方形和420块正三角形地板砖，问：铺设这样的图案，最多能铺多少层?请说明理由．
实践探究题 普通