1.
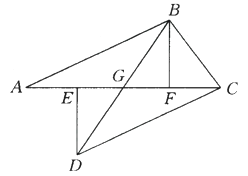
如图,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,若AB=CD,试证明BD平分EF.
【考点】
直角三角形全等的判定-HL;
全等三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优