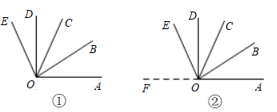1.
如图:∠AOB∶∠BOC∶∠COD=2∶3∶4,射线OM、ON分别平分∠AOB与∠COD,又∠MON=90°,则∠AOB为( )
A.
20°
B.
30°
C.
40°
D.
45°
【考点】
角的运算;
角的大小比较;
角平分线的概念;