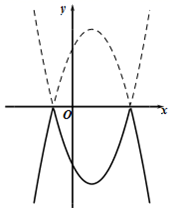
1.
如图,已知抛物线 与直线
与直线 交于
交于 两点.则关于
两点.则关于 的不等式
的不等式 的解集是( )
的解集是( )

A.
 或
或 B.
B.
 或
或 C.
C.
 D.
D.

【考点】
二次函数与一次函数的综合应用;