1.
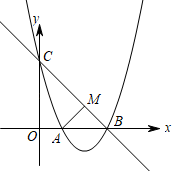
若二次函数 与x轴只有一个交点,且经过
与x轴只有一个交点,且经过 和
和 .
.
(1)
用含a的代数式表示m;
(2)
若点 也在该二次函数的图象上,求该二次函数的解析式.
也在该二次函数的图象上,求该二次函数的解析式.
【考点】
二次函数图象与坐标轴的交点问题;
二次函数y=ax²+bx+c的性质;
二次函数与一元二次方程的综合应用;