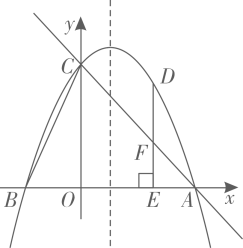
1.
已知抛物线 与
与 轴相交于
轴相交于 两点,与
两点,与 轴相交于点
轴相交于点 .
.
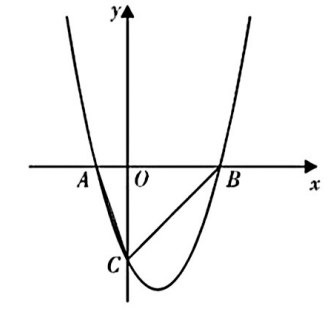
(1)
求b,c的值;
(2)
P为第一象限抛物线上一点, 的面积与
的面积与 的面积相等,求直线AP的解析式;
(3)
在(2)的条件下,设E是直线BC上一点,点
的面积相等,求直线AP的解析式;
(3)
在(2)的条件下,设E是直线BC上一点,点 关于AE的对称点为点
关于AE的对称点为点 , 试探究,是否存在满足条件的点
, 试探究,是否存在满足条件的点 , 使得点
, 使得点 恰好落在直线BC上,如果存在,求出点
恰好落在直线BC上,如果存在,求出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【考点】
待定系数法求二次函数解析式;
二次函数-动态几何问题;
二次函数的实际应用-几何问题;
能力提升
真题演练