0 返回首页
1. 【问题解决】

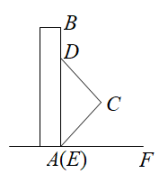
如图1，点C为线段AB上一点，∠A＝∠B＝90°，AD＝BC，BE＝AC，连接CD、CE、DE.

(1) 求证：△ACD≌△BEC.
(2) 判断△CDE是哪种特殊三角形，并说明理由.
(3) 【拓展延伸】

如图2，点C为线段AB上一点，∠A＝∠B＝45°，CD⊥CE.当CD＝CE时，求的值.
【考点】
等腰直角三角形; 三角形全等的判定-AAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
实践探究题 普通
能力提升
真题演练
换一批
1.    

(1) 某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ， 直线l经过点A ， BD⊥直线l ， CE⊥直线l ， 垂足分别为点D、E ． 证明：DE＝BD+CE ．
(2) 组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ， 其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
(3) 数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ， 求证：I是EG的中点．
实践探究题 困难
2. （1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在中， ， 直线l经过点A，直线l，直线l，垂足分别为点D、E．证明： ．

（2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在中， ， D、A、E三点都在直线l上，并且有 ， 其中α为任意锐角或钝角．请问结论是否成立？如成立，请你给出证明；若不成立，请说明理由．

（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过的边、向外作等腰和等腰 ， 是边上的高，延长交于点I，求证：I是的中点．

        
实践探究题 困难
3.  在证明等腰三角形的判定定理时，甲、乙、丙三位同学各添加一条辅助线，方法如图所示你能用哪位同学添加辅助线的方法完成证明，请选择一种方法补全证明过程．                                                                   

等腰三角形的判定定理：
如果一个三角形有两个角相等，那么这两个角所对的边也相等简写成“等角对等边”
已知：如图，在中，求证： ．

甲的方法：
证明：作的平分线交于点 ．

乙的方法：
证明：作于点 ．

丙的方法：
证明：取中点 ， 连接 ．

实践探究题 普通