1.
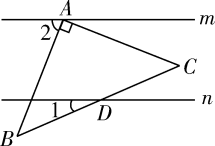
古希腊数学家埃拉托色尼是第一个测算地球周长的人,他在当时的城市塞恩(图中的点A)竖立的杆子在某个时刻没有影子,而此时在500英里以外的亚历山大(图中的点B)竖立杆子的影子却偏离垂直方向约 , 由此他得出
, 由此他得出 , 那么
, 那么 的度数也就是
的度数也就是 的
的 , 所以从亚历山大到塞恩的距离也就等于地球周长的
, 所以从亚历山大到塞恩的距离也就等于地球周长的 . 其中“
. 其中“ ”所依据的数学定理是( )
”所依据的数学定理是( )

A.
两直线平行,内错角相等
B.
两直线平行,同位角相等
C.
两直线平行,同旁内角互补
D.
内错角相等,两直线平行
【考点】
平行线的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练