1.
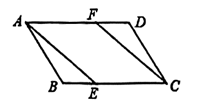
如图,四边形  是边长为1的正方形,点
是边长为1的正方形,点  是射线
是射线  上的动点(点
上的动点(点  不与点
不与点  ,点
,点  重合),点
重合),点  在线段
在线段  的延长线上,且
的延长线上,且  ,连接
,连接  ,将
,将  绕点
绕点  顺时针旋转90°得到
顺时针旋转90°得到  ,连接
,连接  .设
.设  ,四边形
,四边形  的面积为
的面积为  ,下列图象能正确反映出
,下列图象能正确反映出  与
与  的函数关系的是( )
的函数关系的是( )
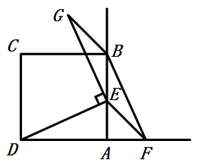
A.
 B.
B.
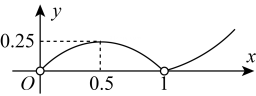 C.
C.
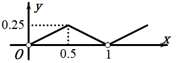 D.
D.
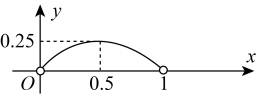
 B.
B.
 C.
C.
 D.
D.

【考点】
平行四边形的判定与性质;
二次函数-动态几何问题;
基础巩固
能力提升
变式训练
拓展培优