如图，AB＝AC，AD＝AE，∠BAC＝∠DAE.

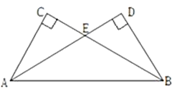
1. 如图，AB＝AC，AD＝AE，∠BAC＝∠DAE.

(1) 求证：△ABD≌△ACE；

(2) 若∠1＝25°，∠2＝30°，求∠3的度数.

【考点】

全等三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题容易

1. 如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC不动，△ADE绕点A旋转，连接BE，CD，F为BE的中点，连接AF.

(1) 如图①，当∠BAE＝90°时，求证：CD＝2AF；

(2) 当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．

综合题困难

2. 已知在△ABC与△ABD中，AC=BD，∠C=∠D=90°，AD与BC交于点E，

(1) 求证AE=BE；

(2) 若AC=3，AB=5，求△ACE的周长．

综合题普通

3. 如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．

(1) 求证：△ABE≌DCE；

(2) 当∠AEB=50°，求∠EBC的度数？

综合题普通