1.
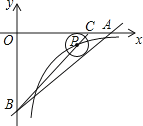
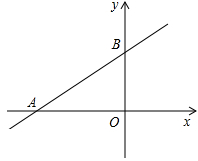
如图，已知直线 
的函数表达式为 
，它与 
轴、 
轴的交点分别为A、B两点.
(1)
求点A、B的坐标；
(2)
设F是 轴上一动点，⊙P经过点B且与 轴相切于点F，设⊙P的圆心坐标为P(x，y)，求y与 之间的函数关系；
(3)
是否存在这样的⊙P，既与 轴相切，又与直线 相切于点B？若存在，求出圆心P的坐标；若不存在，请说明理由.
【考点】
切线的性质;
