1.
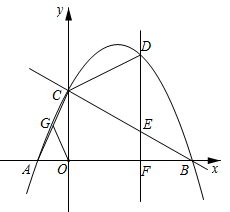
抛物线y=﹣  x2+
x2+  x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<
x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<  )上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
(1)
点A,B,D的坐标分别为,,;
(2)
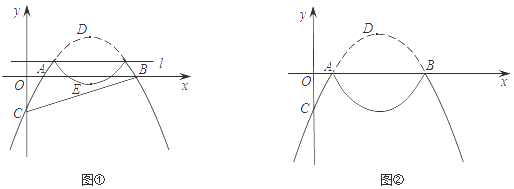
如图①,抛物线翻折后,点D落在点E处.当点E在△ABC内(含边界)时,求t的取值范围;
(3)
如图②,当t=0时,若Q是“M”形新图象上一动点,是否存在以CQ为直径的圆与x轴相切于点P?若存在,求出点P的坐标;若不存在,请说明理由.
【考点】
二次函数图象与坐标轴的交点问题;
二次函数与一次函数的综合应用;
二次函数的实际应用-几何问题;
能力提升
真题演练