1.
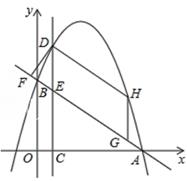
某建筑物的窗户如图所示,上半部分 是等腰三角形,
是等腰三角形, ,
,  , 点
, 点 、
、 、
、 分别是边
分别是边 、
、 、
、 的中点;下半部分四边形
的中点;下半部分四边形 是矩形,
是矩形, , 制造窗户框的材料总长为16米(图中所有黑线的长度和),设
, 制造窗户框的材料总长为16米(图中所有黑线的长度和),设 米,
米, 米.
米.

(1)
求 与
与 之间的函数关系式,并求出自变量
之间的函数关系式,并求出自变量 的取值范围;
(2)
当
的取值范围;
(2)
当 为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.
为多少时,窗户透过的光线最多(窗户的面积最大),并计算窗户的最大面积.
【考点】
二次函数与一次函数的综合应用;
二次函数的实际应用-几何问题;
能力提升
真题演练